하... 이 문제는 일단 약 한 달 전에 풀이했던 문제고, 미리 정리를 제대로 안했던 것이 매우 후회가 되는...
(이걸 제대로 이해했다면 아마 1월 라피신 마지막 시험 마지막 문제도 풀어낼 수 있지 않았을까하는 네네...ㅠ)
이 문제는 이전에 많이 풀어 봤던 최단거리 구하기가 아니라 트리의 지름이 될 수 있는 최대거리를 구해야하는 문제이다.
하지만 풀이 방식은 거의 그대로이다. dfs탐색에서 최단 거리가 아니라 최대 거리를 갱신하며 탐색한다는 정도? 마지막에 한 단계 더 생각해야 하는 점은 있다!
코드 ->
#include <iostream>
#include <vector>
#include <algorithm> //fill함수
using namespace std;
//map배열에 1~v정점에 연결된 간선정보 pair<정점번호, 거리> vector로 넣기
vector<pair<int, int>> map[100001];
//방문 노드 체크
bool visited[100001];
//가장 긴 거리, 노드 전역변수로 선언
int maxd, maxv;
//DFS 탐색
void DFS(int vn, int dist) {
//방문 표시
visited[vn] = true;
//max값 갱신
if (maxd < dist) {
maxd = dist;
maxv = vn;
}
// map[vn] 중 방문하지 않은 정점을 DFS로 돌면서 maxd갱신
for (int i = 0; i < map[vn].size(); i++) {
pair<int, int> tmp = map[vn][i];
if (!visited[tmp.first]) {
DFS(tmp.first, dist + tmp.second);
}
}
}
int main() {
//입출력 속도 향상
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
maxd = 0;
int v;
cin >> v;
for (int i = 0; i < v; i++) {
visited[i + 1] = false;
int idx, vn, dis;
cin >> idx >> vn;
while (vn != -1) {
cin >> dis;
map[idx].push_back({vn, dis});
cin >> vn;
}
}
DFS(1, 0);
fill(visited + 1, visited + v + 1, false);
DFS(maxv, 0);
cout << maxd;
return 0;
}일단 정점번호에 1부터 v까지 주어진다고 해서 노드1(무조건 존재함)을 시작으로 dfs탐색을 했다. 하지만 거기서 끝나면 안된다... 1의 노드에서 출발하면 탐색의 결과인 maxn은 지름에서 가장 끝점은 맞지만 1은 끝점이라는 보장이 없기 때문.
주어진 예제에서 예외 경우의 수를 만들어 봤다.
- 주어진 예제 그대로라면 1부터 dfs탐색 한 번만 해도 문제가 없다.
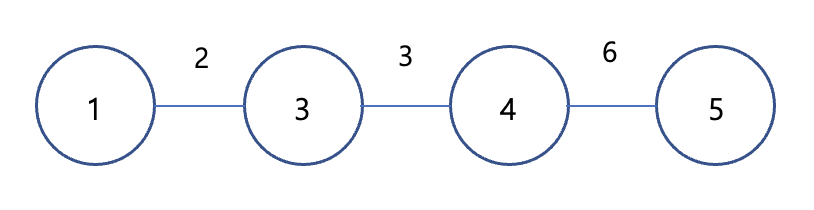
- 하지만 이런 경우라면...

만약 노드 6, 7이 저런 식으로 더 연결되어 있다면 첫 dfs탐색에서는 지름에 포함되는 간선에 노드 6, 7이 포함되어 있지 않을 것이고 올바른 답을 낼 수 없다.
결론적으로, 탐색을 노드 1부터 시작하긴 했지만 그건 임의의 점에서 출발한 것 뿐이고 지름의 한 쪽 끝 점만 구해진 것이다. 따라서 visited 배열을 초기화하고 다시 역으로 maxn부터 dfs탐색을 한 번 더 해주어야 한다!
'baekjoon' 카테고리의 다른 글
| [baekjoon 백준] 1043 - 거짓말 : c++ 문제풀이 (1) | 2024.03.08 |
|---|---|
| [baekjoon 백준] 5430 - AC : c++ 문제풀이 (0) | 2022.11.11 |
| [baekjoon 백준] 1107 - 리모컨 : c++ 문제풀이 (0) | 2022.09.30 |